Bài 7: Quantum Support Vector Machine

Nội dung

1. Giới thiệu
2. Quantum Support Vector Machine
3. Code

Giới thiệu

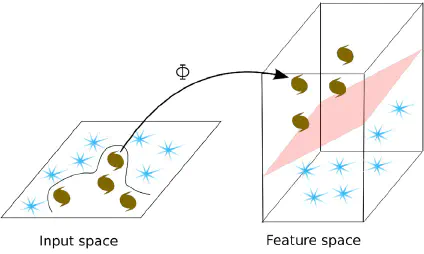
Support Vector Machine, hay thường được gọi là SVM, có lẽ là một trong những thuật toán học máy có giám sát phổ biến nhất. Về cơ bản, trong bài toán phân loại hai classes (binary classification problem), chúng sẽ cần đi tìm một siêu phẳng phân chia chính xác hai classes đó. Tuy nhiên tồn tại rất nhiều mặt phẳng như vậy (Hình 1). Thuật toán SVM sẽ giúp chúng ta đi tìm mặt phẳng tối ưu nhất. Về chi tiết về SVM, bạn có thể tham khảo ở đây

Cho véc-tơ $x_i \in \mathcal{R}^{N}$ với nhãn $y_i = \{1,-1\}$ tương ứng, với $i = 1,…,M$ và $M$ là số điểm dữ liệu cho trước. Từ đó thuật toán SVM sẽ tìm một mặt siêu phẳng sao khoảng cách giữa các đường biên của từng class tương ứng là lớn nhất, như Hình 2.

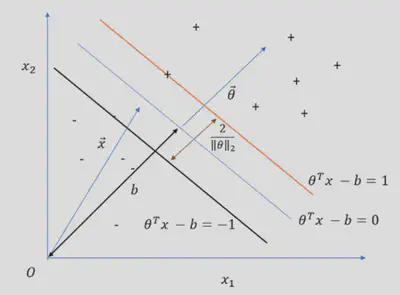
Giả sử mặt siêu phẳng được biểu diễn bằng một véc-tơ tham số $\overrightarrow{\theta} \in \mathcal{R}^n$ và $b$, thì mình có véc-tơ $\overrightarrow{x} \in \mathcal{R}^n$ nằm trên mặt siêu phẳng này sẽ được biểu diễn dưới dạng: $$ \theta^{T}x - b = 0 $$ Từ đây, thuật toán SVM sẽ tìm $\overrightarrow{\theta}$ và $b$ sao cho khoảng cách $\frac{2}{||\theta ||_2}$ lớn nhất và tách riêng được hai đường biên theo: $$ \left\{ \begin{array}{rcl} \theta^{T}x - b \geq 1 & \forall y = 1 \\ \theta^{T}x - b \leq 1 & \forall y = -1 \end{array}\right. $$ $$ \longrightarrow y(\theta^{T}x - b) \geq 1 $$ Như vậy, bài toán tối ưu của chúng ta sẽ được triển khai như sau:

$$ \min_{\theta} \frac{1}{2} \|\theta \|_2 \quad (1) $$ sao cho $$ \quad y_i(\theta^{T}x_i - b) - 1 \geq 0; \forall i= \{1,2,...,M \} $$ Đến đây chúng ta thường đơn giản hóa bài toán tối ưu này theo dạng dual rồi áp dụng kernel method để giải. Tuy nhiên, cách trên lại dường như không thể áp dụng trên một thuật toán lượng tử vì độ phức tạp của chúng (mọi người có thể đọc rõ hơn về phần này ở Chapter 5 Santanu Pattanayak et.al.). Mặt khác, một dạng biến đổi khác được gọi là least square SVM có thể giải quyết được vấn đề này trong máy tính lượng tử và từ đó phát triển lên thành thuật toán QSVM như hiện tại.

Quantum Support Vector Machine

Khác với dual form của SVM, dạng least square SVM biến đổi ràng buộc $y_i(\theta^T x_i -b) \geq 1$ thành: $$ y_i(\theta^T x_i -b) = 1-e_i $$ trong đó sai số $e_i \geq 0$ với mỗi điểm dữ liệu tương ứng $(x_i, y_i)$. Ở dưới dạng biến đổi này, ngoài việc tìm min của $\frac{1}{2} ||\theta||_2$ như ở công thức (1), thì trong bài toán tối ưu, mình cũng cần giảm thiểu sai số, $e_i$. Do đó bài toán tối ưu mới của least square SVM tương đương:

$$ \min_{\theta} \frac{1}{2} \|\theta \|_2 + \frac{\gamma}{2}\sum_{i=1}^{M} e_i^2 \quad (2) $$ sao cho $$ y_i(\theta^{T}x_i - b) = 1 - e_i; \forall i= \{1,2,...,M \}; e_i \geq 0 \quad (*) $$

Vì $y_i \in \{1, -1\}$, nên $y_i^2 = 1$, thay vào (*), ta có $$ y_i^2(\theta^{T}x_i - b) = y_i - y_ie_i $$ $$ \Leftrightarrow \theta^{T}x_i - b = y_i - y_ie_i $$ $$ \Leftrightarrow y_i - (\theta^{T}x_i - b) = y_ie_i $$ Mà $y_i \in \{1, -1\}$, nên $y_ie_i = e_i$ hoặc $-e_i$. Do đó mình hoàn toàn xóa bỏ ràng buộc $e_i \geq 0$ trong (*) để có ràng buộc mới
$$ y_i - (\theta^{T}x_i - b) = e_i ; \forall i= \{1,2,...,M \} \quad (**) $$

Từ đây để giải bài toán tối ưu trên, mình sử dụng phương pháp nhân tử Lagrange (Lagrange multipliers): $$ \min L(\theta, b, \alpha, e) = \frac{1}{2} \|\theta \|_2 + \frac{\gamma}{2}\sum_{i=1}^{M} e_i^2 - \sum_{i=1}^{M}\alpha_i[(\theta^Tx_i-b)-y_i+e_i] $$ trong đó $\alpha_i$ là các nhân tử Lagrange. Giải bài toàn tìm min trên ta được: $$ \left\{ \begin{array}{rcl} \nabla_{\theta} L = 0 \\ \frac{\partial L}{\partial b} = 0 \\ \nabla_{e} L = 0 \\ \frac{\partial L}{\partial \alpha_i} = 0 \end{array}\right. $$ $$ \Leftrightarrow \left\{ \begin{array}{rcl} \theta - \sum_{i=1}^{M}\alpha_ix_i = 0 \quad (3)\\ \sum_{i=1}^{M}\alpha_ix_i = 0 \quad (4)\\ \gamma e - \alpha = 0 \quad (5) \\ (\theta^Tx_i-b)-y_i+e_i = 0 \quad (6) \end{array}\right. $$ Thay giá trị của $\theta$ và $e$ ở (3) và (5) vào (6), ta có: $$ y_i = (\sum_{j=1}^{M}\alpha_jx_j)x_i-b - \alpha_i \gamma^{-1} \quad (7) $$ Gọi $K$ mà một ma trận $M\times M$ với các phần tử $K_{ij} = x_i x_j$. Ta có thể biến đổi công thức (4) và (7) dưới dạng phương trình: $$ \left[ \begin{array}{cc} 0 & \mathbb{1}^T \\ \mathbb{1} & K + \gamma^{-1} \end{array} \right] \left[ \begin{array}{c} -b \\ \alpha \end{array} \right] = \left[ \begin{array}{c} 0 \\ Y \end{array} \right] $$ $Y$ là một ma trận cột với các phân tử tương ứng là nhãn $y_i$.

Từ đây mình đẫ biến đổi bài toán SVM thành một dạng của phương trình $Ax = b$, do đó thuật toán HHL của Bài 5 sẽ được sử dụng để hoàn thành thuật toán QSVM của chúng ta.

Code

Với thuật toán QSVM, mình có thể triển khai nó một cách đơn giản với vài dòng code sử dụng IBM’s Qiskit.

Ở đây, mình sẽ dụng một bộ dư liệu thật của bài toán dư đoán ung thư vú (breast cancer). Để đơn giản hóa, mình sử dụng thuật toán PCA để giảm chiều dữ liệu về 2

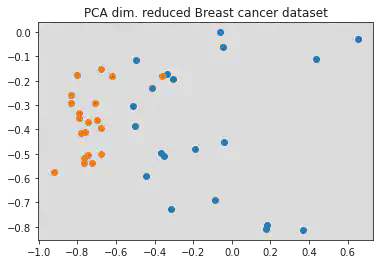
Bài toán QSVM có thể triển khai như sau:

# Gọi các modules cần thiết
import matplotlib.pyplot as plt
import numpy as np

from qiskit import BasicAer
from qiskit.circuit.library import ZZFeatureMap
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.algorithms import QSVM
from qiskit.aqua.utils import split_dataset_to_data_and_labels, map_label_to_class_name

# Set seed cho chương trình
seed = 10599
aqua_globals.random_seed = seed

# Ở đây, mình sẽ sử dụng một mạch có sẵn từ qiskit, được gọi là ZZFeatureMap, để mã hóa dữ liệu
feature_map = ZZFeatureMap(feature_dimension=feature_dim, reps=2, entanglement='linear')

# Khởi tạo thuật toán QSVM
qsvm = QSVM(feature_map, training_input, test_input)

# Chạy mô phỏng bằng qiskit
backend = BasicAer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, shots=1024, seed_simulator=seed, seed_transpiler=seed)
result = qsvm.run(quantum_instance)

print(f'Testing success ratio: {result["testing_accuracy"]}')

Testing success ratio: 0.85

Chạy chương trình trên, thuật toán QSVM mang cho chúng ta độ chính xác là 85%.

Source code cho phần này có thể được tìm thấy ở đây.

Để chứng thực kết quả trên, mình so sánh với thuật toán SVM của thư viện sklearn.

from qiskit.aqua.algorithms import SklearnSVM
result = SklearnSVM(training_input, test_input).run()

print(f'Testing success ratio: {result["testing_accuracy"]}')

Testing success ratio: 0.85

Có thể thấy thuật toán QSVM mang lại kết quả có độ tính xác tương đương với SVM thông thường. Tuy nhiên, đây là kết quả từ một thí nghiệm mô phỏng và không có nhiễu (noiseless environment). Trên thực tế, kết quả có thể bị ảnh hưởng bởi những tác động từ nhiễu trong máy tính lượng tử.

Cảm ơn mọi người đã đọc bài.