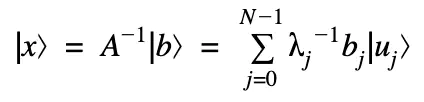
Cuối cùng trong bộ 3 bài viết về các subroutines của thuật toán lượng tử, mình muốn đề cập tới thuật toán Harrow-Hassidim-Lloyd (hay HHL) được đặt theo tên của ba tác giả đã giới thiệu thuật toán ¹. Thuật toán HHL được phát triển nhằm giải quyết phương trình hoặc hệ phương trình tuyến tính bằng máy tính lượng tử, hay nói cách khác thuật toán sẽ giải phương trình:

Theo phương pháp truyền thống, phương trình trên có thể được giải bằng cách nghịch đảo ma trận $A$ và có kết quả là $x=A^{-1}b$. Tuy nhiên, việc tính toán ma trận nghịch đảo tốn rất nhiều tài nguyên khi ma trận $A$ lớn. Với một cách phố biến nhất như là Gaussian emilination, ta cần tới độ phức tạp $O(N^3)$ để nghịch đảo một ma trận $N\times N$; hay tiên tiến hơn với thuật toán conjugate gradient có độ phức tạp $O(Nsk \log{1/\epsilon})$, ở đó $s$ là tỷ lệ phấn tử có giá trị $0$ trong ma trận $A$ (sparsity proportion), $k$ là tỷ số giữa giá trị riêng lớn nhất và giá trị riêng nhỏ nhất, và cuối cùng là $\epsilon$ ký hiệu cho độ sai số của thuật toán. Nhưng với HHL, thuật toán có thể xử lý vẫn đề ma trận nghịch đảo với $O(\log{(N)}s^2k^2/\epsilon)$.

Ở đây, mình sẽ cùng mọi người phân tích rõ hơn về thuật toán này.

Nội dung

1. Thuật toán HHL
2. Source Code

Thuật toán HHL

Thuật toán HHL đặc biệt quan trọng cho các bài toán của QML, vì như mọi người đã biết hầu hết các thuật toán machine learning đều đi học tham số $\theta$ theo phương trình $y = \theta^{T}x$. Do đó, ta hoàn toàn có thể áp dụng HHL trong việc tìm $\theta$ trong các bài toán của machine learning.

Thực chất vấn đề lớn nhất của HHL là làm sao đưa ma trận $A$ của phương trình $Ax = b$ vào máy tính lượng tử. Như mình đã đề cập rất nhiều từ các bài viết trước, các phép biến đổi trong máy tính lượng tử phải từ ma trận đơn nhất (unitary matrix). Do đó, ta không thể trực tiếp dùng $A$ để biến đổi, nhưng may thay mọi ma trận đơn nhất đều có thể biểu diễn theo công thức tổng quát: $U = e^{iHt}$, trong đó $H$ là ma trận Hermitian, và $t$ biểu thị thời gian (mọi người có thể xem chứng minh ở Box 1).

Như vậy, ta hoàn toàn có thể sử dụng một kỹ thuật nhỏ để biến $A$ thành một ma trận Hermitian, $\tilde{A}$, để có một ma trận đơn nhất $U = e^{i\tilde{A}t}$. Ở đây, mình có thể biểu diễn $\tilde{A}$ dưới dạng:

Dễ dàng có thể thấy $\tilde{A} =\tilde{A}^{\dagger}$ nên $\tilde{A}$ là một ma trận Hermitian. Như vậy thay vì trực tiếp giải $x = A^{-1}b$, mình sẽ đi giải quyết bài toán $\ket{x} = \tilde{A}^{-1}\ket{b}$

Mặt khác, nếu ta phân rã trị riêng của $\tilde{A}$ ta được $V\Lambda V^{-1}$ trong đó $V$ gồm các véc-tơ cột là véc-tơ riêng của $\tilde{A}$ và $\Lambda$ có các phần tử đường chéo là các giá trị riêng của $\tilde{A}$. Mà $\tilde{A} = \tilde{A}^{\dagger}$ nên dễ dàng có thể thấy $VV^{\dagger} = I$ nên $V^{-1} = V^{\dagger}$. Do đó, ta có thể viết công thức phân rã trị riêng của $\tilde{A}$ như sau: $$ \tilde{A} = \sum_{i} \lambda_i \ket{v_i}\bra{v_i} $$

Ở đó, các véc-tơ riêng $\ket{v_i}$ tạo thành hệ cơ sở trực giao (orthonormal basis), hay $\left\langle v_i| v_i \right\rangle = 1$ và $\left\langle v_i| v_j \right\rangle = 0 $. Nên ta cũng có thể biểu diễn được $\ket{b}$ theo $\ket{v_i}$: $$ \ket{b} = \sum_{i} \beta_i \ket{v_i} \quad (2) $$

Thay (1) và (2) vào $\ket{x} = \tilde{A}^{-1}\ket{b}$, ta được:

$$ \ket{x} = \sum_{i} \frac{1}{\lambda_i} \ket{v_i}\bra{v_i} \sum_{i} \beta_i \ket{v_i} $$ $$ = \sum_{i} \frac{\beta_i}{\lambda_i} \ket{v_i} \quad (3) $$

Từ kết quả trên, có thể thấy nhiệm vụ của thuật toán HHL sẽ biến đổi đến trạng thái $\sum_{i} \frac{\beta_i}{\lambda_i} \ket{v_i}$. Sau đây, mình sẽ phân tích từng bước một trong những bước triển khai của HHL.

Bước 1: Khởi tạo Như minh họa ở Hình 1, thuật toán HHL có đầu vào gốm có 3 thanh ghi:

• Thanh ghi Ancilla gồm 1 qubit được khởi tạo bằng $\ket{0}_{ANC}$. Qubit này sẽ được sử dụng để hỗ trợ cho phép quay (rotation) từ $\lambda_i\ket{v_i}$ thành $\frac{1}{\lambda_i}\ket{v_i}$.

• Thanh ghi thứ hai sẽ chịu trách nhiệm lưu giữ thông tin về giá trị riêng từ kết quả của thuật toán Phase estimation - QPE. Và tương tự với Bài 4, số qubits được dùng ở thanh ghi này sẽ phụ thuộc vào sai số của thuật toán QPE. Các qubits ở đây cũng được khởi tạo với giá trị $\ket{0}_{W}$.

• Thanh ghi cuối cùng mã hóa giá trị của $\ket{b}$. Mọi biến đổi sau này mình sẽ giả sử $\ket{b}$ đã được chuẩn hóa để đơn giản trong quá trình trình bày các công thức. Trong trường hợp khác $\ket{b}$ hoàn toàn có thể chuẩn hóa theo: $\ket{b_{norm}} = \frac{\ket{b}}{\left\langle b| b \right\rangle^{1/2}}$

Như vậy, mình có thể suy ra trạng thái đầu vào của bài toán từ 3 thanh ghi trên có dạng:

Bước 2: Phase Estimation

Như mình trình bày ở Bài 4, thuật toán QPE sẽ giúp mình tìm được giá trị riêng, $\lambda_i$, của ma trận đơn nhất $U = e^{i\tilde{A}t}$ tương ứng với véc-tơ riêng cho trước $\ket{v_i}$. Tuy nhiên, vì ta chưa biết giá trị của các véc-tơ riêng $\ket{v_i}$ của $U$, nên thay vào đó ta có thể dùng véc-tơ $\ket{b} = \sum_{i} \beta_i \ket{v_i}$ cho thuật toán QPE.

Xét ma trận $\tilde{A}$ có phân rã trị riêng bằng $\sum_{j}\lambda_j \ket{v_j}\bra{v_j}$, ta có phân rã trị riêng của $e^{i\tilde{A}t}$ là: $$ e^{i\tilde{A}t} = \sum_j e^{i\lambda_j t} \ket{v_j}\bra{v_j} $$

Do đó nếu mình áp dụng thuật toán QPE với ma trận đơn nhất $e^{i\tilde{A}t}$ trên véc-tơ $\ket{b}$, mình sẽ thu được trạng thái của $\tilde{\lambda} = \frac{\lambda_i t}{2\pi}$. Như vậy kết quả thu được sau khi sử dụng QPE là: $$ \ket{\psi_0} \xrightarrow[]{QPE} \ket{\psi_1} = \ket{0}_{ANC} \otimes \sum_j \beta_j \ket{\tilde{\lambda_j}} \otimes \ket{v_j} $$

Bước 3: Nghịch đảo giá trị riêng (Eigenvalues Inversion)

Theo như công thức (3), mình cần tính nghịch đảo của $\lambda_i$. Ta có thể đạt được điều này bằng cách áp dụng phép quay của ancilla qubit ($\ket{0}_{ANC}$) theo trục $y$ với một góc $\theta_j$ phụ thuộc vào trạng thái của $\ket{\tilde{\lambda_j}}$. Ở đây,

$$ \theta_j = 2 \sin^{-1} \frac{C}{{\lambda_j}}, $$ trong đó $C$ là một hằng số bất kỳ. Do đó phép quay $R_y(\theta_j)$ được biểu diễn dưới dạng:

Phép quay này sẽ biến đổi ancilla qubit ($\ket{0}_{ANC}$) thành:

Mà $\theta_j = 2 \sin^{-1} \frac{C}{\lambda_j}$, nên $\sin(\frac{\theta_j}{2}) = \frac{C}{\lambda_j}$ và $\cos(\frac{\theta_j}{2}) = \sqrt{1 - \frac{C^2}{\lambda_j^2}}$. Thay kết quả này vào công thức (4), ta được: $$ R_y(\theta_j)\ket{0}_{ANC} = \sqrt{1 - \frac{C^2}{{\lambda_j}^2}}\ket{0} + \frac{C}{\lambda_j}\ket{1} $$

Như vậy sau bước 3, kết quả của cả ba thanh ghi là:

Bước 4: Reverse Phase Estimation

Vì mình đã đạt được $\frac{1}{\lambda_j}$, nên thực chất bài toán của chúng ta không còn cần tới $\ket{\lambda_j}$ ở thanh ghi thứ 2. Mình thực hiện phép nghịch đảo của thuật toán QPE. Các phép biến đổi trong máy tính lượng tử là từ các ma trận đơn nhất (unitary matrix) nên luôn tồn tại ma trận nghịch đảo của chúng. Do đó ta hoàn toàn có thể thiết kế phép biến đổi nghịch đảo $QPE^{-1}$ như Hình 1 bằng cách nghịch đảo các phép toán của QPE. Từ đó, mình thu được:

Vì các qubits ở thanh ghi thứ hai được đưa vê trạng thái khởi tạo ban đầu $\ket{0}_W$ nên mình hoàn toàn có thể bỏ qua thanh ghi này ở trong bài toán của chúng ta:

Bước 5: Measurement Ở bước cuối cùng này, mình thực hiện phép đo trên ancilla qubit và chỉ lấy kết quả khi ancilla qubit có giá trị bằng $\ket{1}$. Khi đó, từ công thức (5) ta có thể thấy kết quả của thuật toán HHL là: $$ \ket{\psi_{final}} = C \sum_{j} \frac{\beta_j}{\lambda_j} \ket{v_j} $$

Từ đây, ta có thể đấy $\ket{\psi_{final}}$ chính là kết quả $\ket{x} = \sum_{j} \frac{\beta_j}{{\lambda_j}} \ket{v_j}$ mà chúng ta cần tìm kiếm, trong đó các hằng số $C$ và $t$ có thể tinh chỉnh sao cho $C=1$. Nghe có vẻ hơi mâu thuẫn nhưng thực chất để tính toán được $\lambda_j$ ta phần nhiều dựa vào kết quả của $\ket{\tilde{\lambda_j}}$, và chính nó phụ thuộc vào giá trị của $t$. Nên thay vì ngay từ đầu chọn $C = 1$, ta cần tinh chỉnh cả 2 giá trị $C$, $t$ để thu được kết quả chính xác nhất.

Có thể thấy thuật toán HHL có rất nhiều triển vọng cho sự phát triển của QML, tuy nhiên khả năng tính toán vượt trội của HHL cũng là vấn đề của nó. Câu hỏi ở đây là làm thế nào để lấy được thông tin từ véc-tơ đầu ra $\ket{x}$. Phổ thông nhất có lẽ mọi người sẽ sử dụng phép đo (measurement) toàn bộ số qubits của $\ket{x}$, nhưng với bộ dữ liệu có số chiều lớn, việc thực hiện phép đo trên toàn bộ qubits sẽ tốn nhiều tài nguyên tính toán vì No-cloning Theorem trong máy tính lượng tử. Nên với mỗi lần thực hiện phép đo thuật toán lượng tự cần phải tạo lại các phép biến đổi từ đầu.

Do đó người ta thường dùng thuật HHL theo 2 cách như sau mà vẫn giữ được khả năng tính toán vượt trội của nó:

• Chiếu trạng thái của $\ket{x}$ trên một không gian nhỏ hơn và tính toán giá trị kỳ vọng (expectation value) của $\ket{x}$ trên không gian đó: $$ \mathbb{E}_O(x) = \bra{x}O\ket{x} $$ Trong đó $O$ được gọi là observable có dạng của một ma trận đơn nhất. Các observables, $O$, thường được dùng có thể kể đến như Pauli-X, Pauli-Y, và Pauli-Z tương ứng với phép chiếu lên x-axis, y-axis, và z-axis của Bloch Sphere.

• Sử dụng HHL nhưng một chương trình con subroutine cho các thuật toán khác nhằm tận dụng khả năng tính toán vượt trội của nó.

Source Code

Đâu tiên ta có class HamiltonianSimulation sẽ tạo một trận đơn nhất $U$ từ ma trận Hermitian $\tilde{A}$.

class HamiltonianSimulation(cirq.EigenGate, cirq.testing.SingleQubitGate):
    """
    Class này sẽ tạo ma trận đơn nhất từ một ma trận Hermitian đầu vào _H_ và
    thời gian t.
    """

    def __init__(self, _H_, t, exponent=1.0):
        cirq.testing.SingleQubitGate.__init__(self)
        cirq.EigenGate.__init__(self, exponent=exponent)
        self._H_ = _H_
        self.t = t
        eigen_vals, eigen_vecs = np.linalg.eigh(self._H_)
        self.eigen_components = []
        for _lambda_, vec in zip(eigen_vals, eigen_vecs.T):
            theta = -_lambda_*t / np.pi
            _proj_ = np.outer(vec, np.conj(vec))
            self.eigen_components.append((theta, _proj_))

    def _with_exponent(self, exponent):
        return HamiltonianSimulation(self._H_, self.t, exponent)

    def _eigen_components(self):
        return self.eigen_components

Ở đây, như mình đã đề cập ở công thức (*), hàm trên sẽ tính ma trận đơn nhất $U$ theo $e^{i\tilde{A}t} = \sum_j e^{2\pi i (\frac{\lambda_j t}{2\pi})} \ket{v_j}\bra{v_j}$

Tiếp đến, ta có mô-đun thứ hai là QuantumPhaseEstimation. Đoạn code dưới đây hầu hết sẽ giống với code của Bài 4, tuy nhiên nó được cải tiến để có thể hoạt động với ma trận $U$ bất kỳ.

class ControlledUnitary(cirq.Gate):

    def __init__(self, num_qubits, num_input_qubits, U):
        self._num_qubits = num_qubits
        self.num_input_qubits = num_input_qubits
        self.num_control_qubits = num_qubits - self.num_input_qubits
        self.U = U

    def num_qubits(self) -> int:
        return self._num_qubits

    def _decompose_(self, qubits):
        qubits = list(qubits)
        input_state_qubit = qubits[:self.num_input_qubits]
        control_qubits = qubits[self.num_input_qubits:]

        for i,q in enumerate(control_qubits):
            _pow_ = 2 ** (self.num_control_qubits - i - 1)
            #yield self.U(q, *input_state_qubit)**_pow_
            yield cirq.ControlledGate(self.U**_pow_)(q, *input_state_qubit)
          
class QuantumPhaseEstimation:
    '''
    Class QuantumPhaseEstimation được cải tiến từ code bài 4 (https://github.com/qmlvietnam/CodeforBlog/blob/main/QPE%20(1).ipynb)
    cho ma trận đơn nhất U bất kỳ.
    '''
    def __init__(self,
                 U,
                 input_qubits,
                 num_output_qubits=None,
                 output_qubits=None, initial_circuit=[],measure_or_sim=False):


        self.U = U
        self.input_qubits = input_qubits
        self.num_input_qubits = len(self.input_qubits)
        self.initial_circuit = initial_circuit
        self.measure_or_sim = measure_or_sim

        if output_qubits is not None:
            self.output_qubits = output_qubits
            self.num_output_qubits = len(self.output_qubits)
            
        elif num_output_qubits is not None:
            self.num_output_qubits = num_output_qubits
            self.output_qubits = [cirq.LineQubit(i) for i 
               in range(self.num_input_qubits,self.num_input_qubits+self.num_output_qubits)]
            
        else:
            raise ValueError("Alteast one of num_output_qubits or output_qubits to be specified")
        
        self.num_qubits = self.num_input_qubits+self.num_output_qubits
    
    def inv_qft(self):
        self._qft_= QFT(qubits=self.output_qubits)
        self._qft_.qft_circuit()
        print('print',self._qft_)
        self.QFT_inv_circuit =  self._qft_.inv_circuit
        
    def circuit(self):
        self.circuit = cirq.Circuit()
        self.circuit.append(cirq.H.on_each(*self.output_qubits))
        print(self.circuit)
        print(self.output_qubits)
        print(self.input_qubits)
        print((self.output_qubits + self.input_qubits))
        self.qubits = list(self.input_qubits + self.output_qubits) 
        self.circuit.append(ControlledUnitary(self.num_qubits,
                                         self.num_input_qubits,self.U)(*self.qubits))
        self.inv_qft()
        self.circuit.append(self.QFT_inv_circuit)
        if len(self.initial_circuit) > 0 :
            self.circuit = self.initial_circuit + self.circuit
    
    def measure(self):
        self.circuit.append(cirq.measure(*self.output_qubits,key='m'))
        
    def simulate_circuit(self,measure=True):
        sim = cirq.Simulator()
        if measure == False:
            result = sim.simulate(self.circuit)
        else:
            result = sim.run(self.circuit, repetitions=1000).histogram(key='m')
        return 

class EigenValueInversion triển khai phép nghịch đảo ở Bước 3. Ở đây, như mình đã đề cập giá trị $\theta_j$ bị ràng buộc bởi giá trị của $\ket{\tilde{\lambda_j}}$: $$ \theta_j = 2 \sin^{-1} \frac{C}{{\lambda_j}}, $$

$$ \Leftrightarrow \theta_j = 2 \sin^{-1} \frac{Ct}{{2\pi \tilde{\lambda_j}}}, $$ Từ đó, ta có thuật toán nghịch đảo giá trị riêng được triển khai như sau:

class EigenValueInversion(cirq.Gate):
    """
    Class EigenValueInversion sẽ nghịch đảo giá trị riêng. Ứng với mỗi giá trị riêng,
    ta áp dụng phép xoay R_y tương ứng.
    """

    def __init__(self, num_qubits, C, t):
        super(EigenValueInversion, self)
        self._num_qubits = num_qubits
        self.C = C
        self.t = t
        # Tổng số các giá trị riêng self.N
        self.N = 2**(num_qubits-1)

    def num_qubits(self):
        return self._num_qubits

    def _decompose_(self, qubits):

        base_state = 2**self.N - 1

        for eig_val_state in range(self.N):
            # Với mỗi véc-tơ cở sở của |\tilde{\lambda_j}> ta tính phép xoay R_y(\theta_j) tương ứng 
            eig_val_gate = self._ancilla_rotation(eig_val_state)

            # Xác định qubits của thanh ghi thứ 2 cho phép biến đổi Controlled-R_Y 
            if (eig_val_state != 0):
                base_state = eig_val_state - 1
            qubits_to_flip = eig_val_state ^ base_state
            for q in qubits[-2::-1]:
                if qubits_to_flip % 2 == 1:
                    yield cirq.X(q)
                qubits_to_flip >>= 1

                # Tạo phép biến đổi Controlled-R_Y 
                eig_val_gate = cirq.ControlledGate(eig_val_gate)

            yield eig_val_gate(*qubits)

    def _ancilla_rotation(self, eig_val_state):
        if eig_val_state == 0:
            eig_val_state = self.N
        # Tính \theta_j theo công thức mình đề cập ở trên
        theta = 2*math.asin(self.C * self.N * self.t / (2*np.pi * eig_val_state))
        
        return cirq.ry(theta)

Từ 3 mô-dun trên, mình có để xây dựng thuật toán HHL một cách hoàn chỉnh

class HHL:

    def __init__(self, hamiltonian, initial_state=None, initial_state_transforms=None, qpe_register_size=4, C=None, t=1):
        """
        :param hamiltonian: ma trận Hermitan đầu vào 
        :param C: C
        :param t: t
        :param initial_state: véc-tơ |b> đầu vào
        """
        self.hamiltonian = hamiltonian
        self.initial_state = initial_state
        self.initial_state_transforms = initial_state_transforms
        self.qpe_register_size = qpe_register_size # số qubit của thanh ghi số 2 cho thuật toán QPE
        self.C = C
        self.t = t

        const = self.t/np.pi
        self.t = const*np.pi
        if self.C is None:
            self.C = 2*np.pi / (2**self.qpe_register_size * t)

    def build_hhl_circuit(self):
        # Khởi tạo cấu trúc mạch cho thuật toán QFT. 
        # Về sau các phép biến đổi sẽ được thêm vào bằng circuit.append()
        self.circuit = cirq.Circuit()
        # Khởi tạo Ancilla qubit = |0> cho thanh ghi thứ nhất
        self.ancilla_qubit = cirq.LineQubit(0)
        # Khởi tạo các qubits của thanh ghi thứ 2 có giá trị |0>
        self.qpe_register = [cirq.LineQubit(i) for i in range(1, self.qpe_register_size+1)]

        # khởi tạo các qubits mã hóa véc-tơ |b>. Nếu initial_state_transforms = None,
        # véc-tơ |b> được cho giá trị là |0>
        if self.initial_state is None:
            self.initial_state_size = int(np.log2(self.hamiltonian.shape[0]))
            if self.initial_state_size == 1:
                self.initial_state = [cirq.LineQubit(self.qpe_register_size + 1)]
            else:
                self.initial_state = [cirq.LineQubit(i) for i in range(self.qpe_register_size + 1,
                                               self.qpe_register_size + 1 + self.initial_state_size)]
        for op in list(self.initial_state_transforms):
            print(op)
            self.circuit.append(op(self.initial_state[0]))

        # Tạo ma trận đơn nhất
        self.U = HamiltonianSimulation(_H_=self.hamiltonian, t=self.t)
        # Quantum Phase Estimation của ma trận U và véc-tơ |b>
        _qpe_ = QuantumPhaseEstimation(input_qubits=self.initial_state,
                                       output_qubits=self.qpe_register, U=self.U)
        _qpe_.circuit()
        print(dir(_qpe_))
        print('CIRCUIT',_qpe_.circuit)
        self.circuit += _qpe_.circuit
        # Nghịch đảo giá trị riêng bằng hàm EigenValueInversion
        _eig_val_inv_ = EigenValueInversion(num_qubits=self.qpe_register_size + 1, C=self.C, t=self.t)
        self.circuit.append(_eig_val_inv_(*(self.qpe_register + [self.ancilla_qubit])))
        
        print(self.circuit)
        # Nghịch đảo các phép toán của QPE
        self.circuit.append(_qpe_.circuit**(-1))
        # Thực hiện phép đo trên ancilla qubit
        self.circuit.append(cirq.measure(self.ancilla_qubit,key='a'))
        # Thêm các observables để tính giá trị kỳ vọng
        self.circuit.append([
            cirq.PhasedXPowGate(
                exponent=sympy.Symbol('exponent'),
                phase_exponent=sympy.Symbol('phase_exponent'))(*self.initial_state),
            cirq.measure(*self.initial_state, key='m')
        ])

    def simulate(self):
      # # Mô phỏng chương trình trên máy tính lượng tử và in ra kết quả
        simulator = cirq.Simulator()

        # Khởi tạo các observables: Pauli-X, Pauli-Y, và Pauli-Z 
        params = [{
            'exponent': 0.5,
            'phase_exponent': -0.5
        }, {
            'exponent': 0.5,
            'phase_exponent': 0
        }, {
            'exponent': 0,
            'phase_exponent': 0
        }]

        results = simulator.run_sweep(self.circuit, params, repetitions=5000)

        for label, result in zip(('X', 'Y', 'Z'), list(results)):
            expectation = 1 - 2 * np.mean(
                result.measurements['m'][result.measurements['a'] == 1])
            print('{} = {}'.format(label, expectation))

Để thí nghiệm thuật toán HHL này, mình sẽ lấy ví dụ các tham số như sau: $$ \tilde{A}\! =\! \left( \begin{array}{cc} 4.302\! -\! 6.016\!\times\! 10^{-8}j & 0.235\! +\! 9.344\!\times\! 10^{-1}j\\ 0.235\! -\! 9.344\!\times\! 10^{-1}j & 0.584\! +\! 6.016\!\times\! 10^{-8}j \end{array} \right) $$ $$ \ket{b} = R_z(1.276359)R_x(1.276359)\ket{0} $$ $$ t = 0.358166 \times \pi $$ $$ n = 4 $$ $$ C = \frac{ 2 \pi}{(2^nt )} $$

Với các observables: Pauli-X, Pauli-Y, và Pauli-Z, thì mình mong chờ kết quả tương ứng thu được là: $(0.144130, 0.413217, -0.899154)$.

So với kết quả thu được từ thuật toán HHL trên:

X = 0.19298245614035092
Y = 0.4145995747696669
Z = -0.8652207591014718

Ta thấy thuật toán HHL mang lại kết quả khá sát so với kết quả chúng ta mong đợi. Mọi người có thể thử tăng độ chính xác bằng cách tăng giá trị $n$ trên.

Toàn bộ code của thuật toán HHL ở đây.

Cảm ơn mọi người đã đọc bài.