Trong bài này, mình đi qua một phương pháp xử lý bài toán nearest neighbour bằng thuật toán quantum. Bài viết dưới đây sẽ dựa vào bài báo gốc: Implementing a distance-based classifier with a quantum interference circuit, nếu ai muốn tìm hiểu sâu hơn về ý tưởng này thì có thể ghé qua.

Nội dung

1. Squared-Distance Classifier
2. Quantum Squared-Distance Classifier
3. Kết luận
4. Source Code

Squared-Distance Classifier

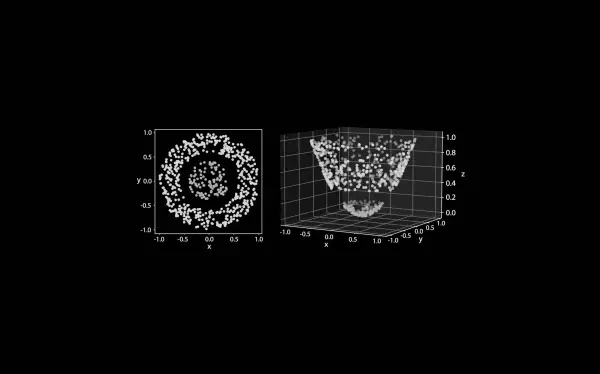
Ở đây, mình xét ví dụ bài toán phân loại tập data Titanic. Giả sử tập data được biểu diễn dưới dạng:

$$ \mathcal{D} = \Big\{ ({\bf{x}}^1, y^1), \ldots ({\bf{x}}^M , y^M) \Big\}, $$

trong đó các véc-tơ đầu vào 2 chiều: ${ {\bf{x}}^m = ({x_0}^m, {x_1}^m)^T}, m = 1,2,…,M$ tượng trưng cho một hành khách trên chuyến tàu Titanic đã bị nhấn chìm vào năm 1912. Trong đó $x_0$ là giá vé trong khoảng từ 0 đến 10,000 đô la, và $x_1$ là số hiệu cabin trong khoảng từ 1 đến 2,500. Ứng với mỗi một véc-tơ đầu vào là nhãn $y^m = {0,1}$ tương ứng để chỉ ra hành khách đó đã sống sót hay không.

Nếu từng tìm hiểu qua về Machine Learning, chắc hẳn các bạn đã nghe hoặc đọc qua về thuật toán nearest neighbour: với mỗi véc-tơ đầu vào mới, thì nhãn của nó sẽ được quyết định bởi điểm dữ liệu gần nhất với nó. Có nhiều cách để xác định những điểm dữ liệu gần nhất đó nhưng phổ biến là Euclidean distance. Do vậy, ta có cách tính hệ số cho việc gán nhãn véc-tơ $\tilde{x}$ mới theo nhãn của $x^m$: $$ \gamma_m = 1-\frac{1}{c}|\tilde{{\bf x}}-{\bf x}^m|^2, $$ trong đó $c$ là hằng số. Hệ số càng cao chứng tỏ $\tilde{{\bf x}}$ càng gần $x^m$. Gọi $\tilde{y}$ là nhãn được gán cho $\tilde{{\bf x}}$, ta có xác xuất $p_{\tilde{{\bf x}}}(\tilde{y}=1)$ là tổng trung bình hệ số của $M_1$ điểm dữ liệu mà có nhãn là $1$: $$ p_{\tilde{{\bf x}}}(\tilde{y}=1) = \frac{1}{\chi}\frac{1}{M_1} \sum_{m|y^m=1}(1-\frac{1}{c}|\tilde{{\bf x}}-{\bf x}^m|^2) $$ Tương tự như vậy, $p_{\tilde{{\bf x}}}(\tilde{y}=0)$ là tổng trung bình hệ số của các điểm dữ liệu mà có nhãn là $0$. Trong đó $\frac{1}{\chi}$ là normalizing factor sao cho $p_{\tilde{{\bf x}}}(\tilde{y}=0)+p_{\tilde{{\bf x}}}(\tilde{y}=1)=1$.

Áp dụng phương pháp ta thấy Passenger 3 sẽ gần với Passenger 1 hơn so với Passenger 2 (Fig 1.2), và mô hình sẽ đưa ra dự đoán là $1$ tương ứng với survival.

Quantum Squared-Distance Classifier

Giờ hãy xử lý bài toàn này bằng phương pháp ‘quantum’.

Bước 1: Data preprocessing and Encoding

Đầu tiên chúng ta sẽ đi tới một câu hỏi kinh điển “Làm sao có thể biểu diễn dữ liệu trên máy tính lượng tử?”. Nếu như trên máy tính truyền thống các thông tin như ảnh sẽ thường được biển diễn trên không gian RBG có giá trị từ 0 đến 255, hay chúng ta có Word Embedding để biểu thông tin dạng văn bản thành các véc-tơ, thì vấn đề của các thuật toán lượng tử cũng như vậy. Thực chất, chủ đề về việc mã hóa thông tin trên không gian lượng tử (Quantum Embedding) vẫn đang được cộng đồng nghiên cứu quan tâm đặc biệt trong lĩnh vực Quantum Machine Learning. Nếu các bạn quan tâm đến chủ đề này có thể xem qua paper này để biết rõ hơn về các cách mã thông tin trong QML và sự quan trọng của nó. Mình sẽ làm một bài viết chi tiết hơn về chủ đề này trong tương lai.

Quay lại với bài toán của chúng ta, mình sẽ áp dụng một phương pháp gọi là Amplitude Embedding - một phương pháp rất phố biến trong QML: Cho $X \in \mathbb{R}^N$ là một véc-tơ đơn nhất ($||X|| = 1$), ta có thể mã hóa $X$ bằng $n$ qubits dưới dạng: $$ \ket{\psi_X} = \sum_{i=0}^{N-1}x_i \ket{i}, $$ trong đó $n = \log{N}$. Có thể thấy phương pháp này chỉ tốn $O(\log{N})$ qubits để biểu diễn một véc-tơ $N$ chiều. Hãy lấy ví dụ trong bài toán xử lý ngôn ngữ tự nhiên, giả sử bạn có một text corpus với 10000 từ thì nếu như cách thông thường ta sử dụng One-hot encoding ta sẽ cần tới 10000 bits để mã hóa, nhưng điều này hoàn toán có thể giải quyết với 14 ($\lceil \log{10000} \rceil$) qubits với amplitude embedding.

Từ đây, với mỗi đầu vào $\ket{\psi_{\bf\tilde{x}}}$ mới, bài toán sẽ được khởi tạo dưới dạng:

Trong đó $\ket{m}$ và $\ket{y^m}$ mã hóa cho số thứ tự và nhãn tương ứng của véc-tơ đầu vào thứ $m^{th}$. Tuy nhiên điều chú ý ở đây nằm ở ancilla qubit được kết nối với $\ket{\psi_{\bf\tilde{{x}}}}$ và $\ket{\psi_{\bf{x}^m}}$. Chú ý rằng khi ta thực hiện phép do trên một hoặc một hệ qubits thì qubit(s) sẽ bị collapsed hay terminated. Vậy khi ta chuyển phép đo của $\ket{\psi_{\bf\tilde{{x}}}}$ hay $\ket{\psi_{\bf{x}^m}}$ sang phép đo của một ancilla qubit được kết nối với chúng thì ta vẫn thu được kết quả cần thiết của $\ket{\psi_{\bf\tilde{{x}}}}$ và $\ket{\psi_{\bf{x}^m}}$ mà không cần chấm dứt (terminate) cả hệ thống. Kỹ thuật này rất hay sử dụng ở trong các thuật toán lượng tử và việc kết nối giữa ancilla qubit với hệ thống là chúng ta đang tạo ra entanglement - một tính chất quan trọng khác trong lĩnh vực tính toán lượng tử.

Như vậy với ví dụ Titanic trên ta có:

$$ \ket{\mathcal{D}} = \frac{1}{\sqrt{4}} \Big\{\ket{0}[\ket{0}(0.866\ket{0}+0.5\ket{1})+\ket{1}(0.921\ket{0}+0.39\ket{1})]\ket{1} $$

$$ + \ket{1}[\ket{0}(0.866\ket{0}+0.5\ket{1})+\ket{1}(0.141\ket{0}+0.99\ket{1})]\ket{0} \Big\} $$

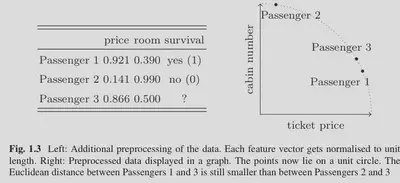
Bước 2: Áp dụng biến đổi Hadamard

Như mình đề cập tới bài viết trước, hầu hết các biến đổi trên máy tính lượng tử là tuyên tính nên việc thực hiện các phép biến đổi là các phép nhân với ma trận biểu diễn tương ứng. Ở đây, ma trận Hadamard có dạng: $$ H = \frac{1}{\sqrt{2}}\left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right) $$

Như vậy, nếu ta áp dụng biến đổi Hadamard cho ancilla qubit ta có:

$$ \ket{\mathcal{D}} \longrightarrow \frac{1}{\sqrt{2M}} \sum_{m=0}^{M-1} \ket{m}\Big(H\ket{0}\ket{\psi_{\bf\tilde{{x}}}} + H\ket{1}\ket{\psi_{\bf{x}^m}}\Big)\ket{y^m} $$

Với những bạn đã đọc qua Bài 1 hoặc với một chút tính toán, chúng ta dễ dàng chứng minh được: $$ H\ket{0} = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1}), H\ket{1} = \frac{1}{\sqrt{2}}(\ket{0}-\ket{1}) $$ Áp dụng công thức trên, ta được: $$ \ket{\mathcal{D}}\! \longrightarrow\! \frac{1}{2\sqrt{M}} \sum_{m=0}^{M-1} \ket{m}\Big(\ket{0}(\ket{\psi_{\bf\tilde{{x}}}}+\ket{\psi_{\bf{x}^m}}) + \ket{1}(\ket{\psi_{\bf\tilde{{x}}}}-\ket{\psi_{\bf{x}^m}})\Big)\ket{y^m} $$

Bước 3: Phép đo

Ở đây ta sẽ cần sử dụng lần lượt 2 phép đo trên ancilla qubit và $\ket{y^m}$. Nhưng trước đó mình sẽ viết lại kết quả thu được sau bước 2: $$ \frac{1}{2\sqrt{M}} \sum_{m=0}^{M-1} \ket{m}\Big(\ket{0}\sum_{i=0}^{N} ({\tilde{{\bf{x}}}}^m_i+{\bf{x}}^m_i)\ket{i} + \ket{1}\sum_{i=0}^{N} ({\tilde{{\bf{x}}}}^m_i-{\bf{x}}^m_i)\ket{i}\Big)\ket{y^m} $$

1. Phép đo trên ancilla qubit: Ở phép đó này, ta sẽ có xác suất $p_0 = \Big(\frac{1}{2\sqrt{M}} \sum_{m=0}^{M-1}\sum_{i=0}^{N} ({\tilde{{\bf{x}}}}^m_i+{\bf{x}}^m_i)\Big)^2 = \frac{1}{4M}\sum_M|{\bf\tilde{x}}+{\bf x}^m|^2$ thu được kết quả là $0$ và tương tự ta thu được kết quả 1 từ ancilla qubit với xác suất $p_1=\frac{1}{4M}\sum_M|{\bf\tilde{x}}-{\bf x}^m|^2$. Tuy nhiên ở đây ta sẽ chỉ lấy kết quả thu được nếu ancilla qubit có giá trị là $0$, hay nói cách khác ta terminate nhánh mà ancilla qubit có trạng thái là $\ket{1}$, ta có: $$ \frac{1}{2\sqrt{Mp_0}} \sum_{m=0}^{M-1} \ket{m}\Big(\ket{0}\sum_{i=0}^{N} ({\tilde{{\bf{x}}}}^m_i+{\bf{x}}^m_i)\ket{i} \Big)\ket{y^m} $$

Ta nhân $p_0$ ở đây để chắc chắn rằng hệ thống của chúng ta vẫn là đơn nhất (unit length).

2. Phép đo trên $\ket{y^m}$ Ta có thể dễ dàng thấy xác suất thu được có giá trị bằng $0$ là: $$ p(y=0) = \frac{1}{4Mp_0}\sum_{m|y^m=0}|{\tilde{{\bf{x}}}+{\bf{x}}^m}|^2 $$

Vì $\tilde{{\bf{x}}}$ hay ${{\bf{x}}}^m$ là đơn nhất nên ta hoàn toàn có thể chứng minh được:

$$ \frac{1}{4Mp_0}\sum_{m|y^m=0}|{\tilde{{\bf{x}}}+{\bf{x}}^m}|^2 = 1 - \frac{1}{4Mp_0}\sum_{m|y^m=0}|{\tilde{{\bf{x}}}-{\bf{x}}^m}|^2 $$

Bài toán sẽ được hoàn toàn đưa về giống với kết quả trường hợp trên máy tính truyền thống mà mình đề cập tới ở trên.

Ta áp dụng bài toán của tập Titanic vào công thức trên ta được: $$ p(y=0) = \frac{1}{4Mp_0}(|0.141+0.866|^2+|0.990+0.5|^2) \approx 0.448, $$

$$ p(y=1) = \frac{1}{4Mp_0}(|0.921+0.866|^2+|0.390+0.5|^2) \approx 0.552, $$

Như vậy có thể thấy kết quả thu được từ thuật toán lượng tử này cũng cho ra kết quả rằng Passenger 3 sẽ sống sót.

Kết luận

Có thể thấy chúng ta hoàn toàn có thể xây dựng một thuật toán lượng tử tương đương trong bài toán distanced-based classifier. Mặc dù ví dụ trên chưa cho chúng ta thấy được quantum advantage nhưng nó giúp mọi người hiểu được cấu trúc chung của một thuật toán lượng tử nói chung và mô hình trong QML nói riêng: Mã hóa (embedding) -> Các phép biến đổi (Transformations) -> Phép đo (Measurement).

Source Code

Mã nguồn trong bài này có thể được tìm thấy tại đây.