Bài 8: Quantum Neural Network

Nội dung

1. Giới thiệu
2. Quantum Neural Network
3. Code

Giới thiệu

Từ những năm 90s, các nhà khoa học đã nghiên cứu sự liên quan của các hiện tượng lượng tử (quantum phenomena) với khả năng nhận thức của con người (“Shadows of the Mind”, Roger Penrose, 1994). Do đó, sự xuất hiện của Quantum Neural Network (hay QNN) dường như là một bước phát triển mới trong việc mô phỏng hệ thống thần kinh của con người khi xử lý thông tin. Mặt khác, những mạng neuron thần kinh truyền thống (classical neural networks) đang dần gặp khó khăn trong các ứng dụng dữ liệu lớn (big data applications). Từ đó các đặc điểm của tính toán lượng tử như quantum parallelism, entanglement, hay interference sẽ được tận dụng để cho ra mô hình hiệu quả hơn.

Từ cuối thế kỷ trước, các nhà vật lý lượng tử đã cho ra ‘quantum versions’ của mạng neuron thần kinh truyền thống. Ở đó, các phép biến đổi (hay các gates) trong quantum circuit được tham số hóa. Do đó Quantum Neural Network thường được ám chỉ tới Parameterized Quantum Circuit. Ở bài viết này, mình sẽ giới thiệu tới mọi người những bước chính để xây dựng cũng như huấn luyện một mô hình QNN.

Quantum Neural Network

Hầu hết các thiết kế hiện nay của QNN đều dựa theo một hệ thống ‘hybrid’ (mô tả ở Hình 1) gồm 2 phần ‘quantum part’ và ‘classical part’. Trong đó chúng ta sẽ xây dựng mô hình và trích xuất kết quả ở ‘quantum part’. Tuy nhiên tham số sẽ được tối ưu bởi những thuật toán ở ‘classical part’ (ví dụ như Gradient Descent, Adam, etc.).

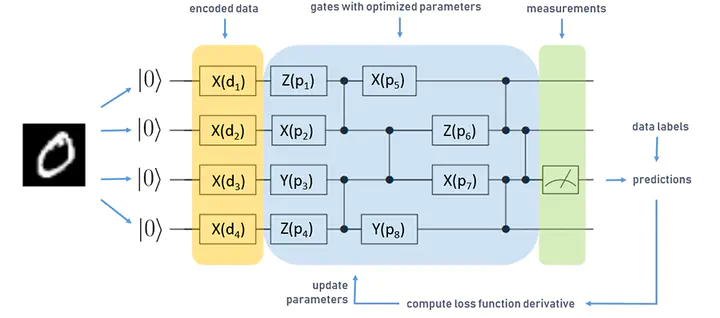
Mô hình QNN thường có 3 bước chính (Hình 2) như hầu hết bài toán mình đã trình bày ở các bài viết trước: data encoder, transformation, và measurement. Sau đây mình sẽ đi chi tiết hơn vào từng bước một:

1. Data Encoder: Cho $\vec{x} \in \mathbb{R}^n$, chúng ta sẽ mã hóa $\vec{x}$ dưới dạng một trạng thái lượng tử (quantum state) $\ket{\psi(x)}$. Nếu như ở các bài viết trước mình đã nói về Amplitude Encoding có thể mã hóa $\vec{x} \in \mathbb{R}^n$ với $\log{n}$ qubits, thì ở bài viết này mình sẽ giới thiệu một kỹ thuật khác: Angle Encoding. Ở đó mỗi thành phần $x_i$ của $\vec{x}$ là tham số của các rotation gates: $$ \ket{\psi(x)} = R(x_1) \otimes R(x_2) \otimes ... \otimes R(x_n) \ket{\psi_0} $$
   Có thể thấy cách mã hóa này cần $n$ qubits cho $\vec{x} \in \mathbb{R}^n$, tuy nhiên với độ phức tạp nhỏ (gồm $n$ one-qubit rotation gates) [Box 1] kỹ thuật này vẫn thường xuyên được sử dụng trong các mô hình QNN.

2. Transformation Bước này đóng vai trò chính cho khả năng của một mô hình QNN. Ở đây các quantum gates sẽ được tham số hóa bởi $\omega \in \mathbb{R}^{n \times 3 \times l}$ như Hình 3 với $l$ là số layers của mô hình. Có thể thấy với mỗi layer sẽ gồm 2 thành phần: rotation and entanglement. Nếu như với rotation, chúng ta thực hiện phép quay $\ket{\psi(x)}$ xung quanh Bloch sphere để học những trạng thái khác nhau của data, thì entanglement sẽ tăng cường khả năng trao đổi thông tin của các qubits có trong $\ket{\psi(x)}$ từ đó giúp mô hình học được những hidden correlation của các features $x_i$ trong $\vec{x}$ (Box 2).
   

   

Hiện tại có rất nhiều thiết kế mô hình Transformation khác nhau, mọi người có thể xem qua bài báo này để tìm hiểu thêm.

3. Measurement Ở đây, chúng ta sẽ trả lời câu hỏi làm sao có để trích xuất những features có ý nghĩa từ quantum state để mình có thể lấy ra output từ chúng. Có lẽ phương pháp measurement phổ biến nhất trong các mô hình QNN là tính giá trị trung bình của observables, Pauli-Z, của một quantum state.

Ta có: $$ Z = \left[ \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right] = \ket{0}\bra{0} - \ket{1}\bra{1} $$

$\Rightarrow$ Giá trị trung bình: $$ \bra{\psi}Z\ket{\psi} = \bra{\psi}\ket{0}\bra{0}\ket{\psi} - \bra{\psi}\ket{1}\bra{1}\ket{\psi} $$ $$ = |\braket{0|\psi}|^2 - |\braket{1|\psi}|^2 = P(0) - P(1) $$ Có thể thấy khi ta lấy giá trị trung bình của observables $Z$ của quantum state $\ket{\psi}$ ta thu được một hiệu giữa xác suất output có giá trị bằng $0$, $P(0)$ và xác suất output có giá trị bằng $1$, $P(1)$.

Trong bài toán phân loại, mô hình chúng ta sẽ được tối ưu về $1$ tương đương $P(0) = 1$ và $P(1) = 0$ nếu dư liệu đầu vào có nhãn là $0$. Và ngược lại, mô hình tối ưu về $-1$ tương đương $P(0) = 0$ và $P(1) = 1$ nếu dư liệu đầu vào có nhãn là $1$.

4. Tối ưu với quantum circuit:

Vậy làm sao chúng ta có thể tối ưu tham số trong một quantum circuit. Như mình đề cập ở trên, với mô hình hybrid quantum-classical, các tham số sẽ được tối ưu dựa vào thuật toán của ‘classical part’(Hình 1) như Gradient Descent hay Adam, etc. Vậy câu hỏi đưa ra rằng liệu có sự khác biệt giữa cách tính gradient của ‘classical parameters’ và ‘quantum parameters’. Với mô hình NN truyền thống, nếu gradient của tham số được tính dựa theo Chain Rule thì với QNN, ta có kỹ thuật Paramter shift rule.

Với Paramter shift rule, gradient của tham số $\theta$ trong hàm $f(\theta)$ được tính bằng: $$ \nabla_{\theta}f = r[f(\theta + s) - f(\theta + s)] $$ Với $r$ và $s$ được chọn dựa trên cách ta xây dựng hàm $f$. Nếu các bạn muốn tìm hiểu sâu hơn thì có thể đọc bài báo này.

Code

Mình đã đi qua đầy đủ các thành phần để xây dựng một thuật toán QNN, giờ chúng ta sẽ đi chi tiết hơn làm thế nào để triển khai một mô hình QNN với Pennylane

from itertools import chain
from sklearn import datasets
from sklearn.utils import shuffle
from sklearn.preprocessing import minmax_scale
from sklearn.model_selection import train_test_split
import sklearn.metrics as metrics

import pennylane as qml
from pennylane import numpy as np
from pennylane.templates.embeddings import AngleEmbedding
from pennylane.templates.layers import StronglyEntanglingLayers
from pennylane.optimize import GradientDescentOptimizer

# ---------------------------LOAD DATA------------------------------------------------
# load the dataset
iris = datasets . load_iris ()

# shuffle the data
X , y = shuffle ( iris . data , iris . target , random_state =0)

# select only 2 first classes from the data
X = X[y <=1]
y = y[y <=1]

# normalize data
X = minmax_scale (X , feature_range =(0 , np . pi ))

# split data into train + validation and test
X_train_val , X_test , y_train_val , y_test = train_test_split (X , y , test_size =0.2)

# ------------------------------------DEFINE MODEL---------------------------------------
# number of qubits is equal to the number of features
n_qubits = X.shape[1]

# quantum device handle
dev = qml.device("default.qubit" , wires = n_qubits )

# quantum circuit
@qml.qnode(dev)
def circuit(weights,x= None):
  AngleEmbedding (x , wires = range(n_qubits))
  StronglyEntanglingLayers(weights , wires = range( n_qubits ))
  return qml.expval(qml.PauliZ(0))

# variational quantum classifier
def variational_classifier ( theta , x= None ):
  weights = theta [0]
  bias = theta [1]
  return circuit( weights , x=x) + bias

def cost ( theta , X , expectations ):
  e_predicted = np.array([ variational_classifier ( theta , x= x) for x in X ])
  loss = np.mean(( e_predicted - expectations )**2)
  return loss

# ------------------------------------TRAIN----------------------------
# number of quantum layers
n_layers = 3

# split into train and validation
X_train , X_validation , y_train , y_validation = train_test_split( X_train_val , y_train_val , test_size =0.20)

# convert classes to expectations : 0 to -1, 1 to +1
e_train = np.empty_like ( y_train )
e_train[y_train == 0] = -1
e_train[y_train == 1] = +1

# select learning batch size
batch_size = 5

# calculate numbe of batches
batches = len(X_train) // batch_size

# select number of epochs
n_epochs = 5

# draw random quantum node weights
theta_weights = np.random.random(StronglyEntanglingLayers.shape(n_layers=n_layers, n_wires=n_qubits)) 
theta_bias = 0.0
theta_init = ( theta_weights , theta_bias ) # initial weights

# train the variational classifier
theta = theta_init


# start of main learning loop
# build the optimizer object
pennylane_opt = GradientDescentOptimizer()

# split training data into batches
X_batches = np.array_split(np .arange(len( X_train )) , batches )
for it , batch_index in enumerate ( chain (*( n_epochs * [ X_batches ]))):
  # Update the weights by one optimizer step
  batch_cost = lambda theta : cost ( theta , X_train[ batch_index ], e_train [ batch_index ])
  theta = pennylane_opt.step( batch_cost , theta )
  # use X_validation and y_validation to decide whether to stop
# end of learning loop

# ----------------------------------------VALIDATION------------------------------------------
# convert expectations to classes
expectations = np.array ([ variational_classifier( theta , x=x ) for x in X_test ])
prob_class_zero = ( expectations + 1.0) / 2.0
y_pred = (prob_class_zero <= 0.5)

print(metrics.accuracy_score ( y_test , y_pred ))
print(metrics.confusion_matrix ( y_test , y_pred ))

Đầu tiên, với hàm circuit() mình định nghĩa mô hình QNN của mình như sau:

1. Data Encoder: Như mình đề cập ở trên, mình sẽ sử dụng kỹ thuật AngleEmbedding. Mọi người có thể dễ dàng import nó với pennylane: pennylane.templates.embeddings.AngleEmbedding.
2. Transformation: Mình sử dụng mô hình như đã miêu tả ở Hình 3 với built-in function của pennylane là pennylane.templates.layers.StronglyEntanglingLayers (chi tiết hơn ở đây)
3. Measurement: Cuối cùng mình tính giá trị trung bình (expectation values) của Pauli-Z với pennylane.expval()

Chạy chương trình trên mình có kết quả accuracy_score=1.0 và confusion_matrix:

Chú ý rằng vì output của mô hình trong khoảng $[-1,1]$, nên khi thực hiện bước validation mình sẽ chuyển về $[0,1]$ nên ta mới có bước prob_class_zero = ( expectations + 1.0) / 2.0.

Mọi người có để download code ở đây

Cảm ơn mọi người đã đọc bài.