Bài 4: Important Subroutine 2 - Quantum Phase Estimation
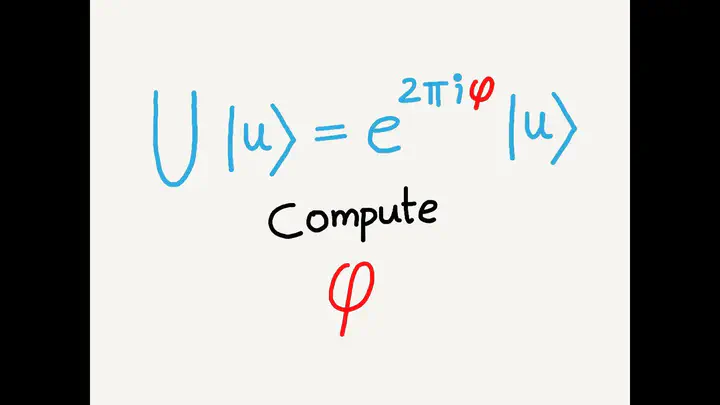
Nội dung
Quantum Phase Estimation
Cho một ma trận đơn nhất (unitary matrix), $\mathcal{U}$, ta cần phải tìm giá trị riêng tương ứng với véc-tơ riêng $\ket{\psi}$ của ma trận $\mathcal{U}$. Vì $\mathcal{U}$ là một ma trận đơn nhất nên khá dễ dàng cho mình chứng minh được các giá trị riêng $\lambda$ của $\mathcal{U}$ có độ lớn là $1$ (mọi người có thể xem chứng minh ở Box 1). Do đó, $\lambda$ hoàn toàn có thể viết dưới dạng $e^{2\pi i \phi}$, $0\leq \phi < 1$, vì $\lambda^{*} \lambda = e^{-2\pi i \phi + 2\pi i \phi} = e^0 = 1$. Như vậy, thuật toán Quantum Phase Estimation (hay QPE) thực chất sẽ đi tính $\phi$ cho giá trị riêng $\lambda$.
](/post/important-subroutine-2/circuit_huc47373d4e794d44fd5d3937ab331d6cf_50019_e3d96adbcc7732115428a8fd72b34728.webp)
Cấu trúc mạch của thuật toán QPE được minh họa ở Hình 1. Thuật toán sẽ có 2 thành phần chính: với thanh ghi đầu tiên, gồm $n$ qubits được khởi tạo ban đầu bằng $\ket{0}$, chịu trách nhiệm giữ nhưng thông tin về $\phi$ sau khi thuật toán kết thúc; còn thanh ghi thứ 2 mã hóa giá trị của véc-tơ riêng $\ket{\psi}$. Vì giá trị của $\phi$ bất định trong khoảng $[0,1)$ nên có thể thấy rằng giá trị của $n$ dùng để giải mã $\phi$ sẽ linh hoạt tùy thuộc độ chính xác mà chúng ta mong muốn (mọi người có thể xem giải thích ở Box 2).
Box 2: Ta có $\phi \in [0,1)$, tương tự với thuật toán QFT ở Bài 3, mình có thể biểu diễn dưới dạng nhị phân như sau:
$$ \phi = 0.\phi_1\phi_2…\phi_k\phi_{k+1}… $$
Vì $\phi$ chưa xác định nên giả sử ta dùng $n$ qubit để giải mã $\phi$ thì luôn tồn tại giá trị $\epsilon \geq 0$ sao cho
$$ \phi = 0.\phi_1\phi_2…\phi_n + \epsilon $$
Trong đó $\epsilon = 0$ khi và chỉ khi $\phi$ có thể biểu diễn chính xác với $n$ qubits. Do đó độ chính xác của thuật toán QPE sẽ phù thuộc vào mọi người tinh chỉnh giá trị $n$.
Như mọi người có thể thấy ở Hình 1, thuật toán QPE gồm có 3 bước:
Bước 1: Sử dụng cổng Hadamard lên các qubits ở thanh ghi đầu tiên. Vì các qubits được khởi tạo bằng véc-tơ $\ket{0}$ nên: $$ \ket{q^1} = H^{\otimes n} \ket{0}^{\otimes n} = \frac{1}{2^{n/2}} (\ket{0}+\ket{1})(\ket{0}+\ket{1})...(\ket{0}+\ket{1}) $$ $$ = \frac{1}{2^{n/2}} \sum_{k=0}^{2^n-1}\ket{k} $$ Bước 2: Lần lượt biến đổi qubits ở thanh ghi thứ hai với ma trận $\mathcal{U}^{2^{n-m}}$; ở đó, phép biến đổi này sẽ phụ thuộc vào qubit thứ $m$ của thanh ghi đầu tiên, $\ket{q^1_m}$. Nếu $\ket{q^1_m} = \ket{0}$, phép biến đổi sẽ giữ nguyên giá trị của $\ket{\psi}$ ở thanh ghi thứ hai, và nó chỉ thực hiện biến đổi với ma trận $\mathcal{U}^{n-m}$ khi $\ket{q^1_m} = \ket{1}$. Do đó, mình có thể ký hiệu phép đổi này là controlled- $\mathcal{U}^{2^{n-m}}$ (hay $C-U^{2^{n-m}}$ như Hình 1). Như vậy, cổng $C-U^{2^{n-m}}$ sẽ biến đổi bài toán của chúng ta như sau: $$ (C-U^{2^{n-m}}) \ket{\psi} \frac{1}{\sqrt{2}} (\ket{0}+\ket{1}) = \frac{1}{\sqrt{2}} (\ket{\psi}\ket{0}+\mathcal{U}^{2^{n-m}}\ket{\psi}\ket{1}) $$ $$ = \frac{1}{\sqrt{2}} (\ket{\psi}\ket{0}+\lambda^{2^{n-m}}\ket{\psi}\ket{1}) = \frac{1}{\sqrt{2}} (\ket{\psi}\ket{0}+e^{2\pi i \phi 2^{n-m}}\ket{\psi}\ket{1}) $$ $$ = \ket{\psi} \otimes \frac{1}{\sqrt{2}} (\ket{0}+e^{2\pi i \phi 2^{n-m}}\ket{1}) $$ Có thể thấy, phép biến đổi controlled- $\mathcal{U}^{2^{n-m}}$ thực chất không thay đổi trạng thái của thanh ghi thứ hai, $\ket{\psi}$, mà nó sẽ thay đổi trạng thái của qubit $\ket{q^1_m}$. Từ đây bài toán đưa ta về vấn đề giống với thuật toán QFT ở Bài 3.
Giả sử, $\phi$ được biểu diễn dưới dạng nhị phân: $$ \phi = 0.\phi_1\phi_2...\phi_n=\phi_1 2^{-1}+\phi_2 2^{-2}+...+\phi_n 2^{-n} $$ Với m = 1, ta có: $$ \phi 2^{n-1} =\phi_1 2^{n-2}+\phi_2 2^{n-3}+...+\phi_n 2^{-1} $$ $$ \Rightarrow e^{2\pi i \phi 2^{n-1}} =e^{2\pi i \phi_1 2^{n-2}}e^{2\pi i \phi_2 2^{n-3}}...e^{2\pi i\phi_n 2^{-1}} $$ Mặt khác, mình có thể thấy $e^{2\pi i} = 1$ nên $e^{2\pi ik} = 1 \forall k \in \mathbb{Z}$. Từ đó có thể dễ dàng suy ra tất cả các phần tử trong công thức trên đều bằng 1 trừ $e^{2\pi i \phi_n 2^{-1}}$, nên $$ e^{2\pi i \phi 2^{n-1}} = 1.1.1...e^{2\pi i \phi_n 2^{-1}} = e^{2\pi i 0.\phi_n} $$ Tương tự ta cũng có thể suy ra: $$ e^{2\pi i \phi 2^{n-2}} = e^{2\pi i 0.\phi_{n-1}\phi_n} $$ $$ ... $$ $$ e^{2\pi i \phi 2^{0}} = e^{2\pi i 0.\phi_1\phi_2...\phi_{n-1}\phi_n} $$ Như vậy nếu mình tổng hợp những kết quả này ta có trạng thái ở các qubits của $\ket{q^1}$ là: $$ \ket{q^1}\!=\!\frac{1}{2^{\frac{n}{2}}}\!(\!\ket{0}\!+\!e^{2\pi i 0.\phi_n}\ket{1}\!)\!(\!\ket{0}\!+\!e^{2\pi i 0.\phi_{n-1}\phi_n}\ket{1}\!)\!...\!(\!\ket{0}\!+\!e^{2\pi i 0.\phi_1\phi_2...\phi_n} \ket{1}\!)\! $$ Như mình đã chứng minh ở Bài 3, kết quả trên bằng với $\frac{1}{2^{n/2}} \sum_{k=0}^{2^n-1} e^{\frac{2\pi ik\phi}{2^n}} \ket{k}$, và nó chính là kết quả của phép biến đổi Fourier từ $\phi$.
Bước 3: Áp dụng thuật toán nghịch đảo của QFT để biến đổi:
$$
\frac{1}{2^{n/2}} \sum_{k=0}^{2^n-1} e^{\frac{2\pi ik\phi}{2^n}} \ket{k} \longrightarrow \ket{\phi}
$$
Thực chất các phép biến đổi trong máy tính lượng tử là từ các ma trận đơn nhất (unitary matrix) nên luôn tồn tại ma trận nghịch đảo của chúng. Do đó ta hoàn toàn có thể thiết kế phép biến đổi nghịch đảo $QFT^{-1}$ như Hình 1 bằng cách nghịch đảo các phép toán của QFT.
Độ phức tạp của QPE
Như Hình 1, ta có thể thấy thuật toán gồm có $n$ cổng Hadamard, $n$ cổng từ phép biến đổi controlled- $\mathcal{U}^{2^{n-m}}$, và cuối cùng là $O(n^2)$ phép toán từ $QFT^{-1}$. Do đó, thuật toán QPE có độ phức tạp là $O(n^2)$.
Tuy nhiên đó là trong trường hợp lý tưởng khi $\phi$ có thể được biểu diễn với chính xác $n$ qubits. Với sai số $\epsilon$ rất nhỏ, người ta đã chỉ ra rằng thuật toán QPE cần $n \propto O(\log{1/\epsilon})$ qubit và $O(1/\epsilon)$ phép biến controlled- $\mathcal{U}$. Chi tiết về kết luận này mọi người có thể tìm hiểu rõ hơn ở Section 5.2.1 Nielson & Chuang
Source Code
class QPE:
def __init__(self, num_input_state_qubits=3,
num_ancillia_qubits=5,
unitary_transform=None,
U=None,
input_state=None):
# Số qubits của thanh ghi đầu tiên như mình đề cập ở trên
self.num_ancillia_qubits = num_ancillia_qubits
# khởi tạo qubits có giá trị bằng |0> ở thanh ghi thứ nhất
self.output_qubits = [cirq.LineQubit(i) for i in range(self.num_ancillia_qubits)]
# Khởi tạo cấu trúc mạch cho thuật toán.
# Về sau các phép biến đổi sẽ được thêm vào bằng circuit.append()
self.input_circuit = cirq.Circuit()
# véc-tơ riêng |\psi> đầu vào
self.input_state = input_state
if self.input_state is not None:
self.num_input_qubits = len(self.input_state)
else:
self.num_input_qubits = num_input_state_qubits
# khởi tạo qubits để mã hóa véc-tơ |\psi> đầu vào
self.input_qubits = [cirq.LineQubit(i) for i in
range(self.num_ancillia_qubits,
self.num_ancillia_qubits + num_input_state_qubits)]
# Mã hóa |\psi> theo các giá trị của input_state
if self.input_state is not None:
for i, c in enumerate(self.input_state):
if int(c) == 1:
self.input_circuit.append(cirq.X(self.input_qubits[i]))
# Ma trận đơn nhất U đầu vào.
# Ở đây mọi người có thể tùy ý chọn một ma trận đơn nhất bất kỳ cho tham số U,
# ngoài ra ở đây mình đưa ra một vài ví dụ cho U: cổng Identity, X, và Z.
self.unitary_transform = unitary_transform
if self.unitary_transform is None:
self.U = cirq.I
elif self.unitary_transform == 'custom':
self.U = U
elif self.unitary_transform == 'Z':
self.U = cirq.CZ
elif self.unitary_transform == 'X':
self.U = cirq.CX
else:
raise NotImplementedError(f"self.unitary transform not Implemented")
self.circuit = cirq.Circuit()
def phase_1_create_circuit_iter(self):
# Triển khai Bước 1 và Bước 2 như mình đã đề cập ở trên
# Bước 1: Các ancilla qubits bị theo đổi theo cổng Hadamard (cirq.H)
# Bước 2: Áp dụng phép biến đổi C-U^{2^m} trên input_qubits và bị ràng buộc bới các output_qubits
for i in range(self.num_ancillia_qubits):
self.circuit.append(cirq.H(self.output_qubits[i]))
_pow_ = 2**(self.num_ancillia_qubits - 1 - i)
#_pow_ = 2 ** (i)
for k in range(self.num_input_qubits):
print(self.U)
self.circuit.append(self.U(self.output_qubits[i], self.input_qubits[k])**_pow_)
def inv_qft(self):
# Phép nghịch đảo của thuật toán QFT.
# Mình sẽ lấy code của bài trước, mọi người có thể xem qua ở https://github.com/qmlvietnam/CodeforBlog/blob/main/QFT.ipynb
# để đọc rõ hơn các tính nghịch đảo của QFT.
self._qft_ = QFT(qubits=self.output_qubits)
self._qft_.qft_circuit()
def simulate_circuit(self,circ):
# Chạy mô phỏng máy tính lượng tử cho thuật toán
sim = cirq.Simulator()
result = sim.simulate(circ)
return result
Giờ mình sẽ chạy chương trình với cổng $Z$ có dạng $\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right)$ . Có thể ma trận trên có 2 giá trị riêng là $1$ và $-1$ tương ứng với 2 véc-tơ riêng $\ket{0}$ và $\ket{1}$. Nếu mình chạy chương trình trên với véc-tơ riêng $\ket{\psi} = \ket{1}$, chúng ta mong chờ kết quả $e^{2\pi i \phi} = -1 \Leftrightarrow \phi=0.5$.
Với trường hợp trên, mình sẽ dùng 2 qubits cho thanh ghi đầu tiền và 1 qubit để mã hóa véc-tơ riêng $\psi$. Kết quả của chương trình như sau:
qubits: (cirq.LineQubit(0), cirq.LineQubit(1), cirq.LineQubit(2))
output vector: |101⟩
Trong đó ta thấy qubit cuối cùng tương ứng với giá trị của véc-tơ riêng $\psi$ đầu vào. Do đó ta có trạng thái của 2 qubit ở thanh ghi đầu tiên $\ket{q_1q_2}$ là $\ket{10}$ tương ứng cho giá trị của $\phi = 0.q_1q_2 = 1\times2^{-1} + 0\times 2^{-2} = 0.5$. Kết quả này hoàn toàn đúng như những gì ta tìm kiếm.
Mọi người có thể xem toàn bộ code của chương trình trên ở đây.
Cảm ơn mọi người đã đọc bài.