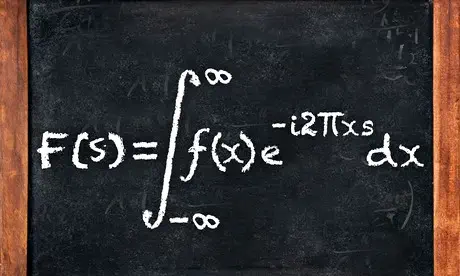
Ở phần này mình sẽ có 3 bài viết nói về 3 subroutines rất quan trọng tạo nên khả năng tính toán vượt trội của thuật toán lượng tử: Quantum Fourier Transform, Quantum Phase Estimation, and HHL algorithm. Những thuật toán trên có mặt nhiều trong các bài toán của QML. Do đó mình tin rằng việc nắm rõ những thuật toán này đầu tiên sẽ giúp các bạn trong việc tìm hiều các thuật toán của QML.

Để khởi đầu trong danh sách trên mình sẽ trình bày thuật toán Quantum Fourier Transform (QFT).

Nội dung

1. Discrete Fourier Transform
2. Quantum Fourier Transform
3. Độ phức tạp của QFT
4. Source Code

Discrete Fourier Transform

Fourier Transform đã và đang xuất hiện trong rất nhiều ứng dụng ở máy tính truyền thống, có thể kể đến như: signal processing hay data compression. Fourier Transform sẽ biến đổi một hàm số hoặc một véc-tơ theo miền thời gian hoặc không gian sang miền tần số. Ví dụ Discrete Fourier Transform (DFT) của một biến rời rạc $\mathcal{X_N} = \{x_0, x_1, …, x_{N-1}\} \in \mathbb{C}^N$ có dạng:

$$ y_k = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} x_j e^{\frac{2\pi ijk}{N}}, $$ Từ đó phép biến đổi sẽ cho ra một chuỗi mới $\mathcal{Y_N} = \{y_0, y_1, …, y_{N-1}\} \in \mathbb{C}^N$ cùng chiều với chuỗi đầu vào.

Mặt khác, mình muốn đề cập tới hàm Kronecker delta, $\delta_{Nj}$, được định nghĩa là một véc-tơ $N$ chiều, có giá trị 1 ở vị trí thứ $j$ và 0 ở các vị trí còn lại. Do đó, mình hoàn toàn có thể coi hàm Kronecker delta là các véc-tơ cơ sở trực chuẩn cho biến $\mathcal{X_N}$:

Không mất tính tổng quát, mình vẫn hoàn toàn có thể lấy hàm Kronecker delta như các véc-tơ cơ sở trực chuẩn $\ket{j}$ sẽ được sử dụng cho thuật toán lượng tử của chúng ta. Nói cách khác, biến $\mathcal{X_N}$ sẽ được mã hóa trong thuật toán lượng tử có dạng ¹: $$ \ket{\mathcal{X_N}} = \sum_{j=0}^{N} x_j \ket{j} $$

Khác phép biến đổi Fourier trên máy tính truyền thống, thuật toán Quantum Fourier Transform sẽ biến đổi các véc-tơ cơ sở trực chuẩn $\ket{j}$:

Và nó tương đương với việc:

$$ \sum_{j=0}^{N-1}x_j \ket{j} \longrightarrow \sum_{k=0}^{N-1} y_k \ket{k} $$ $$ \ket{\mathcal{X_N}} \longrightarrow \ket{\mathcal{Y_N}} $$ Vậy chi tiết đằng sau phép biến đổi này như thế nào, mình sẽ đi tới phần tiếp theo.

Quantum Fourier Transform

Với biến $\mathcal{X_N}$ gồm $N$ phần tử, mình cần $n = \log_2{N}$ qubits để biểu diễn toàn bộ các véc-tơ $\ket{j}$. Ở đây, $j$ được biểu diễn dưới dạng nhị phân $j_1j_2…j_n$ sao cho:
$$ j = j_1 2^{n-1} + j_2 2^{n-2} + ...+ j_n 2^0 $$ Và để thuận tiện hơn trong việc phát triển công thức dưới đây, mình sẽ ký hiệu $0.j_lj_{l+1}…j_m = j_l/2 + j_{l+1}/4+…+j_m/2^{m-l+1}$.

Hãy bắt đầu với qubit đầu tiên $\ket{j_1}$, cổng Hadamard (H gate) biến đổi trạng thái của $\ket{j_1}$ thành $\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{j_1}\ket{1})$. Mình thay $(-1) = e^{\pi i}$, ta được: $$ H\ket{j_1} = \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i (\frac{j_1}{2})}\ket{1}) = \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_1} \ket{1}) $$

Qubit này tiếp đến được biến đổi theo ${\mathbf{R}}_m$ bị ràng buộc bởi giá trị của $j_m$: $$ {\mathbf{R}}_m = \left( \begin{array}{cc} 1 & 0 \\ 0 & e^{\frac{2\pi i j_m}{2^m}} \end{array} \right) $$ Như vậy nếu thực hiện phép biến đổi ${\mathbf{R}}_2$ trên qubit thứ nhất ta được: $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & e^{\frac{2\pi i j_2}{2^2}} \end{array} \right) \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_1} \ket{1}) = \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i (0.j_1+j_2/2^2)} \ket{1}) $$ $$ = \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_1j_2} \ket{1}) $$

Tương tự như vậy ta tiếp tục áp dụng phép biến đổi ${\mathbf{R}}_3$, ${\mathbf{R}}_4$,… ${\mathbf{R}}_n$ mình có trạng thái của qubit thứ nhất được biểu diễn như sau: $$ \ket{j_1} \longrightarrow \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_1j_2...j_n} \ket{1}) $$

Lần lượt như vậy mình dùng các phép biến đổi tương tự cho các qubit tiếp theo, thu được: $$ \ket{j_2} \longrightarrow \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_2...j_n} \ket{1}) $$ $$ \ket{j_3} \longrightarrow \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_3...j_n} \ket{1}) $$ $$ ... $$ $$ \ket{j_n} \longrightarrow \frac{1}{\sqrt{2}}(\ket{0}+e^{2\pi i 0.j_n} \ket{1}) $$

Như vậy nếu mình tổng hợp các kết quả từ $n$ qubits, bài toán của mình sẽ được biểu diễn như sau: $$ \ket{j_1j_2...j_n} \! \longrightarrow \! $$

Và bước cuối cùng mình sẽ swap ² trạng thái của qubit thứ $m$ với qubit thứ $n-m$, hay nói cách khác mình đảo ngược thứ tự trạng thái của các qubit: $$ \frac{1}{2^\frac{n}{2}}(\ket{0}\!+\!e^{2\pi i 0.j_n} \ket{1})(\ket{0}\!+\!e^{2\pi i 0.j_{n-1}j_n} \ket{1})...(\ket{0}\!+\!e^{2\pi i 0.j_1j_2...j_n} \ket{1}) \quad (*) $$

Đến đây, mọi người có thể vẫn còn thắc mắc về kết quả trên nên mình sẽ đi sâu hơn để giải thích kết quả này. Như mình trình bày ở trên thuật toán QFT sẽ biến đổi các véc-tơ cơ sở $\ket{j}$ thành $\frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{2\pi ijk}{N}} \ket{k}$. Nếu mình thay $N = 2^n$ và $\ket{j} = \ket{j_1j_2…j_n}$, ta được: $$ \ket{j_1j_2...j_n} \longrightarrow \frac{1}{2^{n/2}} \sum_{k=0}^{2^n-1} e^{\frac{2\pi ijk}{2^n}} \ket{k} $$ Mặt khác mình cũng có thể biểu diễn $k$ theo dạng nhị phân: $$ k = k_1 2^{n-1}+k_2 2^{n-2}+...+k_n2^0 $$ nên

Thay kết quả này vào công thức trên ta có: $$ \ket{j_1j_2...j_n} \longrightarrow \frac{1}{2^{n/2}} \sum_{k_1=0}^{1}...\sum_{k_n=0}^{1} e^{2\pi ij (\sum_{p=1}^{n}\frac{k_p}{2^p})} \ket{k_1k_2...k_n} $$ $$ \ket{j_1j_2...j_n} \longrightarrow \frac{1}{2^{n/2}} \sum_{k_1=0}^{1}...\sum_{k_n=0}^{1}\prod_{p=1}^{n} e^{2\pi ij (\frac{k_p}{2^p})} \otimes_{p=1}^{n}\ket{k_p} $$

$\otimes$ ký hiệu cho tensor product. Trong các bài toán lượng tử trạng thái của một hệ qubits $\ket{k_1k_2…k_n}$ là tensor product của các trạng thái của từng qubit $\otimes_{p=1}^{n}\ket{k_p}$.

Quay lại bài toán, kết quả chúng ta có thể đơn giải hóa bằng cách đưa các tổng $\sum_{k_i}$ vào trong tensor product: $$ \ket{j_1j_2...j_n} \longrightarrow \frac{1}{2^{n/2}} \otimes_{p=1}^{n} (\sum_{k_p=0}^{1} e^{2\pi ij (\frac{k_p}{2^p})} \ket{k_p}) $$ $$ \ket{j_1j_2...j_n} \longrightarrow \frac{1}{2^{n/2}} \otimes_{p=1}^{n} (\ket{0} + e^{2\pi ij 2^{-p}} \ket{1}) $$ $$ = \frac{1}{2^{n/2}} (\ket{0} + e^{2\pi ij 2^{-1}} \ket{1})(\ket{0} + e^{2\pi ij 2^{-2}} \ket{1})...(\ket{0} + e^{2\pi ij 2^{-n}} \ket{1}) \quad (1) $$ Mà mình lại có $j = j_1 2^{n-1} + j_2 2^{n-2} + …+ j_n 2^0$ nên $j2^{-p}$ sẽ có dạng $$ j2^{-p} = j_1 2^{n-1-p} + j_2 2^{n-2-p} + ...+ j_n 2^{-p} $$ Ta xét trường hợp đầu tiên với p = 1: $$ e^{2\pi ij 2^{-1}} = e^{2\pi i(j_1 2^{n-2} + j_2 2^{n-3} + ...+ j_n 2^{-1})} $$ Mặt khác, mình có thể thấy $e^{2\pi i} = 1$ nên $e^{2\pi im} = 1 \forall m \in \mathbb{Z}$. Từ đó có thể dễ dàng suy ra tất cả các phần tử trong công thức trên đều bằng 1 trừ $e^{2\pi i j_n 2^{-1}}$, nên $$ e^{2\pi ij 2^{-1}} = 1.1.1...e^{2\pi i j_n 2^{-1}} = e^{2\pi i 0.j_n} $$ Tương tự ta cũng có thể suy ra: $$ e^{2\pi ij 2^{-2}} = e^{2\pi i 0.j_{n-1}j_n} $$

$$ ... $$ $$ e^{2\pi ij 2^{-n}} = e^{2\pi i 0.j_1j_2...j_{n}} $$ Thay những kết quả này vào công thức (1), mình thu được: $$ \ket{j}\! \rightarrow\! \frac{1}{2^{n/2}} (\ket{0}\! +\! e^{2\pi i0.j_n} \ket{1})(\ket{0}\! +\! e^{2\pi i0.j_{n-1}j_n} \ket{1})...(\ket{0}\! +\! e^{2\pi i0.j_1j_2...j_n} \ket{1}) $$

Và chính kết quả này giống với kết quả thu được từ thuật toán QFT ở (*). Nói cách khác, với thuật toán QFT, máy tính lượng tử vẫn có khả năng tính toán phép biến đổi Fourier với kết quả tương đương. Tuy nhiên điều thú vị của thuật toán QFT nằm ở khả năng tính toán vượt trội của nó, và sau đây mình sẽ cùng mọi người phân tích rõ hơn về độ phức tạp của QFT.

Độ phức tạp của QFT

Ở đây, mình sẽ coi độ phức tạp tương đương với số phép biến đổi của thuật toán. Đầu tiên với qubit thứ nhất, mình có một cổng Hadamard và $n-1$ cổng $\mathcal{R_m}$, $m = {2,3,…,n}$. Do đó sẽ có tổng $n$ phép biến đổi được thực hiện trên qubit đầu tiên ở bước này. Tương tự như vậy qubit thứ 2 sẽ có $1 + (n-2)=(n-1)$ phép biến đổi, … Tất cả ta có $$ \Theta([n+(n-1)+...+1]+kn) = \Theta(\frac{n(n+1)}{2}+kn) = \Theta(n^2) $$ Trong đó $kn$ là số phép biến đổi cho thao tác đạo ngược (swap) trạng thái của qubits như mình đề cập ở trên. Vì số phép biến đổi của thao tác này luôn tuyến tính với số qubits $n$ sẽ không ảnh hưởng nhiều trong việc phân tích độ phức tạp của QFT, nên mình sẽ có đi sâu về nó. Để rõ ràng hơn mọi người có thể xem cấu tạo của phép swap trên ở đây.

Như vậy với thuật toán Quantum Fourier Transform (QFT) có thể thực hiện phép biến đổi Fourier với độ phức tạp $\Theta(n^2)$. Với một so sánh tương đương với thuật toán Fast Fourier Transform (FFT) cùng cho bài toán của biến rời rạc (discrete fourier transform) có $2^n$ phần tử thì thuật toán FFT sẽ cần tới $\Theta(n2^n)$ phép biến đổi. Có thể thấy QFT mang lại hiệu năng vượt trội so với FFT. Trong khi FFT đang được sử dụng và đóng vai trò rất quan trọng trong nhiều ứng dụng thực tế: nhận diện giọng nói, hình ảnh, …, việc xuất hiện của QFT trong các ứng dụng đó sẽ không dễ dàng, do chúng ta sẽ khó có thể trực tiếp lấy được amplitudes từ kết quả của QFT thông qua phép đo (measurement). Do đó, thay vì trực tiếp chuyển các amplitudes của QFT sang giá trị “classical”, QFT lại thường được sử dụng trong các thuật toán lượng tử khác đặc biệt là các thuật toán QML vì hiệu năng vượt trội của nó.

Source Code

Trên đây, mình đã phân tích những biến đổi và các bước triển khai của thuật toán QFT. Ở phần này, mình sẽ thực hành cùng mọi người bằng cách triển khai thuật toán này bằng Cirq một framework được cung cấp bởi Google Quantum AI giúp người dùng có thể mô phỏng chương trình của máy tính lượng tử sử dụng ngôn ngữ lập trình Python.

Trước khi đi vào chi tiết, mình muốn nhắc lại thuật toán Quantum Fourier Transform sẽ biến đổi các véc-tơ cơ sở trực chuẩn $\ket{j}$:

Do đó với mỗi véc-tơ đầu vào $\ket{j}$, thì thuật toán QFT sẽ cho ra một véc-tơ trực chuẩn mới tương ứng

import cirq
import numpy as np

class QFT:
    """
    Quantum Fourier Transform
    """

    def __init__(self, signal_length=16,
                 basis_to_transform=''):
        
        self.signal_length = signal_length #  Độ dài của chuỗi đầu vào: N
        self.basis_to_transform = basis_to_transform # trạng thái của véc-tơ đầu vào |j>
        
        
        self.num_qubits = int(np.log2(signal_length)) # Số qubit cho QFT
        # Tiếp đến mình sẽ khởi tạo các qubits bằng cirq.LineQubit(). 
        # Các giá  trị được khởi tạo ban đầu bằng |0>
        self.qubits = [cirq.LineQubit(i) for i in range(self.num_qubits)]  
 

        self.qubit_index = 0
        # Khởi tạo cấu trúc mạch cho thuật toán QFT. 
        # Về sau các phép biến đổi sẽ được thêm vào bằng circuit.append()
        self.input_circuit = cirq.Circuit()
        self.circuit = cirq.Circuit()

        for k, q_s in enumerate(self.basis_to_transform):
            if int(q_s) == 1:
                # Nếu phần tử của véc-tơ đầu vào |j> khác |0>. 
                # Ta dùng NOT gate (cirq.X) để để chuyển về |0>.
                self.input_circuit.append(cirq.X(self.qubits[k]))

    def qft_circuit_iter(self):
        # Lần lượt áp dụng cổng H, và phép biến đổi R_m (trong code ta có thể đơn giải hóa thành cổng CZ) 
        # trên từng qubit như Hình 1.
        if self.qubit_index > 0:
            
            for j in range(self.qubit_index):
                diff = self.qubit_index - j + 1
                rotation_to_apply = -2.0 / (2.0 ** diff)
                self.circuit.append(cirq.CZ(self.qubits[self.qubit_index],
                                            self.qubits[j]) ** rotation_to_apply) 
        self.circuit.append(cirq.H(self.qubits[self.qubit_index]))
    
        self.qubit_index += 1

    def qft_circuit(self):

        while self.qubit_index < self.num_qubits:
            self.qft_circuit_iter()
            print(f"Circuit after processing Qubit: {self.qubit_index - 1} ")
            print(self.circuit)

        # Sử dụng cổng SWAP giữa qubit thứ m và qubits thứ n-m 
        self.swap_qubits()

        print("Circuit after qubit state swap:")
        print(self.circuit)

    def swap_qubits(self):
      # Sử dụng cổng SWAP giữa qubit thứ m và qubits thứ n-m 
        for i in range(self.num_qubits // 2):
            self.circuit.append(cirq.SWAP(self.qubits[i], self.qubits[self.num_qubits - i - 1]))

    def simulate_circuit(self):
        # Mô phỏng chương trình trên máy tính lượng tử và in ra kết quả
        sim = cirq.Simulator()
        result = sim.simulate(self.circuit)
        return result

Class QFT của mình sẽ nhận các tham số:

• signal_length: Độ dài của chuỗi đầu vào

• basis_to_transform: Trạng thái của véc-tơ $\ket{j}$ đầu vào

Cấu trúc mạch của thuật toán QFT như Hình 1 được tạo ra từ hàm qft_circuit(). Ở đó các qubits lần lượt bị biến đổi theo cổng Hadamard và $\mathbf{R}_m$ được triển khai ở hàm qft_circuit_iter(). Chú ý ở đấy ta thấy phép biến đổi $\mathbf{R}_m$ bị ràng buộc vào giá trị của phần từ $j_m$ của véc-tơ đầu vào $\ket{j}$: nếu $j_m = 0$ thì $\mathbf{R}_m = I$ và không có tác động nên bài toán, phép biến đổi $\mathbf{R}_m$ chỉ có tác dụng khi và chỉ khi $j_m = 1$, khi đó: $$ {\mathbf{R}}_m = \left( \begin{array}{cc} 1 & 0 \\ 0 & e^{\frac{2\pi i}{2^m}} \end{array} \right) $$ Mặt khác ta có $e^{\pi i} = -1$ $$ \Rightarrow {\mathbf{R}}^{''}_m = \left( \begin{array}{cc} 1 & 0 \\ 0 & (-1)^{\frac{2}{2^m}} \end{array} \right) $$

Do đó, mình hoàn toàn đơn giản hóa phép biến đổi $\mathbf{R}_m$ bị ràng buộc bởi $j_m$ như sau:

Và tiếp đến ta có hàm swap_qubits() sẽ hoàn đổi trạng thái của lần lượt qubit thứ $m$ với $n-m$.

Cuối cùng, mình có thể chạy mô phỏng chương trình này trên máy tính lượng tử với cirq.Simulator().

Với véc-tơ đầu vào $\ket{j} == \ket{0000}$ là một véc-tơ cơ sở của một chuỗi có độ dài $N = 2^4=16$. Theo như công thức (**), chúng ta mong chờ kết quả là một véc-tơ gồm 16 phần tử có giá trị $\frac{1}{4}$. Chương trình trên có kết quả như sau:

output vector: [0.24999997+0.j 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j
 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j
 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j
 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j 0.24999997+0.j]

Có thể thấy kết quả của chương trình này hoàn toàn đúng như chúng ta đã kỳ vọng.

Mọi người có thể xem toàn bộ code của chương trình trên ở đây.

Cảm ơn mọi người đã đọc bài.